Coefficient of Variation
By evaluating the volatility (represented by the usual deviation of returns) to the common return, the coefficient of variation (CV) gives an evaluation of the risk-return relationship inherent in funding choices. Commonplace deviation quantifies the extent to which a inventory’s value tends to deviate from its common return and might be computed utilizing Excel. A decrease CV signifies much less dispersion across the common return, indicating decrease danger per unit of common return. This metric allows buyers to gauge the extent of danger relative to the asset’s returns.
Whereas this device might be utilized to a person’s inventory portfolio, it’s relevant even in case you are a mutual fund investor. Allow us to take the instance of a flexi-cap fund, Fund A, which has a five-star score in our bl.portfolio Star Monitor Scores. A method for an investor to analyse its risk-adjusted returns is by making use of a CV. Evaluating the fund’s three-year efficiency in opposition to the fund’s benchmark S&P BSE 500 TRI, it’s evident that the fund has outperformed its benchmark. Moreover, the fund reveals a CV of 0.49, whereas the benchmark’s CV stands at 0.69. This comparability underscores the comparatively decrease danger related to the fund’s returns.
Whereas the CV is an efficient and easy solution to assess risk-adjusted returns, it encounters limitations when utilized to portfolios which have skilled intervals of destructive returns because the ratio might not present significant insights in such cases. Various risk-adjusted measures such because the Sharpe and Sortino ratios might be helpful right here.
Sharpe and Sortino Ratios
Whereas the Sharpe ratio can be utilized to evaluate any portfolio, in India it’s well-known for measuring risk-adjusted returns in mutual funds. This ratio evaluates how a lot additional return a fund generates over the risk-free price per unit of danger. To compute the Sharpe Ratio, we subtract the risk-free price (typically represented by the in a single day MIBOR price) from the fund’s common return after which divide it by the usual deviation of the fund’s returns.
A better Sharpe Ratio signifies that the fund is adept at producing larger returns for the extent of danger taken. A destructive Sharpe ratio, then again, signifies that the fund has delivered a return that doesn’t compensate buyers for the extent of danger they’ve assumed. That stated, the usual deviation within the Sharpe Ratio consists of each upside and draw back deviation, whereas buyers are primarily involved about draw back danger.
Because of this, buyers can flip to the Sortino ratio, which focuses solely on draw back deviation danger, particularly for these prioritising draw back safety. It employs the identical method because the Sharpe ratio however considers solely the draw back commonplace deviation. Whereas these ratios must be manually computed if you wish to make these assessments in your portfolio, within the case of mutual funds, it’s available in fund factsheets and on-line assets corresponding to BL.Portfolio Mutual Funds rankings,Morningstar, and Value Research online.
Let’s perceive by contemplating two small-cap funds B and C, which have delivered comparable 3-year CAGR trailing returns of round 27 per cent. Their Sortino ratios differ, with Fund B exhibiting a ratio of 0.5 and Fund C at 0.45, as per the Bl.portfolio Star Monitor Scores. The upper Sortino ratio of Fund B signifies that it has generated superior draw back risk-adjusted returns in comparison with Fund C, regardless of their comparable general returns.
Skewness and Kurtosis
Usually, it’s assumed that knowledge distributions, corresponding to inventory returns, are inclined to approximate to regular distribution over a big time period, adhering to the symmetrical bell-shaped curve sample (the statistical idea referred to as the Central Restrict Theorem). Nevertheless, there might be deviations from this norm, influenced by elements corresponding to market dynamics, info asymmetry, danger elements, occurrences of maximum occasions, and buyers’ behavioural biases. Metrics corresponding to skewness and Kurtosis are available in right here.
Skewness serves as a quantitative device to seek out out the course and magnitude of deviations from the common returns. As an example, a negatively skewed distribution (skewness lower than zero), signifies a propensity for frequent small positive aspects alongside occasional excessive losses, thereby signalling potential draw back danger. However, a positively skewed distribution (skewness larger than zero), suggests a better likelihood of small losses juxtaposed with sporadic excessive positive aspects. Nevertheless, if an asset’s return distribution reveals a symmetric sample (bell curve), then there might be no skewness.
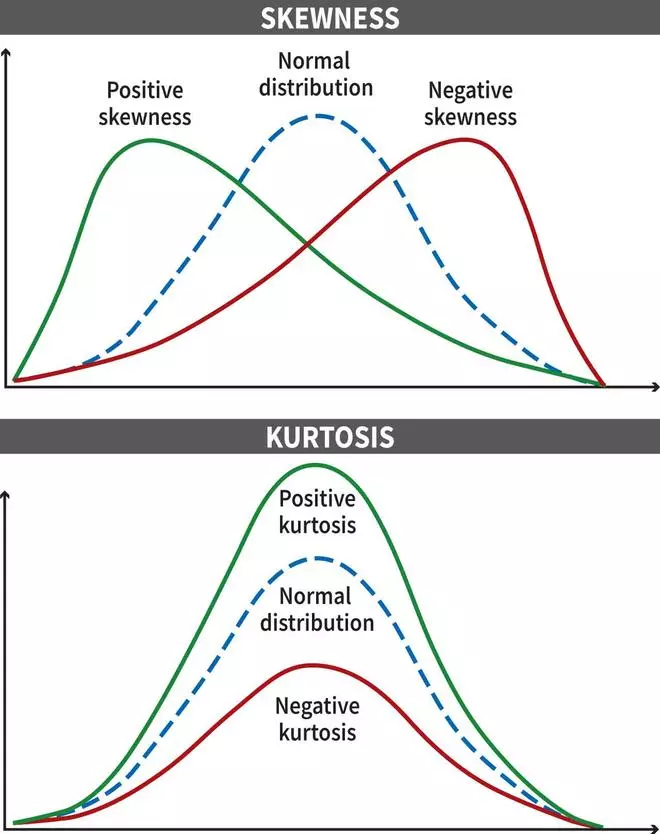
Kurtosis provides one other layer of perception by quantifying the peakedness or flatness of a distribution relative to a standard distribution. When the return knowledge follows a bell-shaped curve, the worth of kurtosis (or extra kurtosis) is the same as three (or zero). Excessive kurtosis values, exceeding three (constructive extra kurtosis), point out a heightened frequency of outliers or excessive occasions that may exert a big affect on returns. Conversely, kurtosis values beneath three (destructive extra kurtosis) recommend a flatter distribution, indicating a diminished probability of maximum deviations from the common return. Normally, constructive extra kurtosis and extra destructive skew in return distributions point out elevated dangers.
Spreadsheet software program can readily calculate these measures. Nevertheless, it’s necessary to notice that Excel computes extra kurtosis which is the same as the worth of kurtosis minus three.
Right here is how skewness and kurtosis might be utilized to investing utilizing examples of the patterns within the varied sectoral indices. Nifty FMCG reveals constructive skewness and low extra kurtosis, aligning with the sector’s non-cyclical/defensive funding nature. Consequently, FMCG shares might enchantment to conservative buyers looking for regular, modest returns amid market volatility. Nifty Healthcare, then again, shows constructive skewness alongside excessive kurtosis, suggesting a sector with a better propensity for irregular constructive returns.
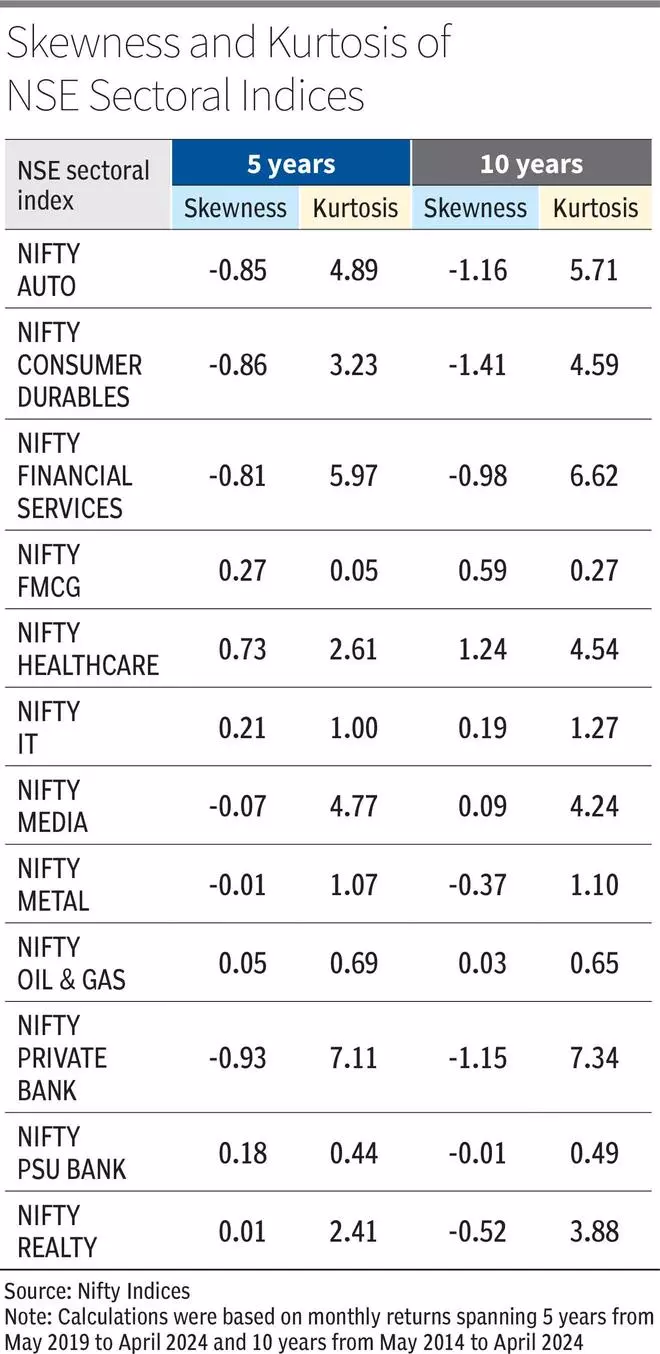
In distinction, sectors corresponding to Nifty Auto, Nifty Shopper Durables, and Nifty Non-public Financial institution display excessive destructive skewness and constructive extra kurtosis. This means a better probability of maximum destructive returns, making these sectors extra vulnerable to larger danger and market fluctuations. As an example, the automotive and shopper durables sectors are delicate to financial cycles and shopper spending patterns, whereas the banking sector faces regulatory, financial, and market dangers. Consequently, buyers with larger danger tolerance ranges might discover these sectors interesting, however they need to additionally issue within the potential for vital draw back danger.
Increasing the scope past fairness investments, conservative buyers might discover gold to be a beautiful asset class. With constructive skewness (0.41), and low extra kurtosis (0.13) during the last 10 years, gold costs have a tendency to indicate extra reasonable positive aspects than losses, with fewer excessive value actions in comparison with different property. This stability makes gold a possible hedge in opposition to inflation and geopolitical uncertainty, enhancing diversification in conservative portfolios. By incorporating property with numerous skewness and kurtosis traits, buyers can mitigate general portfolio danger and improve the potential for secure, risk-adjusted returns.
Worth at Threat
Worth at Threat (VaR) is relevant throughout numerous monetary devices, spanning shares, bonds, and derivatives. It gauges the potential draw back of an funding portfolio, estimating the minimal loss more likely to happen inside a specified time interval with a given likelihood. Whereas retail buyers can profit from VaR, its main customers embody monetary establishments, portfolio managers, and institutional buyers, utilising it to judge and mitigate funding dangers at a portfolio degree.
Although handbook computation of VaR might be complicated, buyers could make use of the VaR margin out there in inventory exchanges. As an example, think about a pattern portfolio comprising 2 shares of Maruti Suzuki, 6 shares of TCS, 12 shares of HUL, and 16 shares of HDFC Financial institution, with a notional worth of round ₹1 lakh (round ₹25,000 in every firm). By inputting these values within the NSE margin calculator, one can see that the each day VaR of this pattern portfolio quantities to round ₹8,999.5 as of Could 2. It needs to be famous that the VaR margin in these exchanges is up to date at common time intervals all through the buying and selling day to replicate market actions.
Sometimes, monitoring a portfolio’s VaR at predefined intervals is essential. If it will increase because of market turbulence, it indicators the necessity to probably modify positions or mitigate danger by diversifying the holdings.
Nevertheless, VaR has its personal set of constraints. Its reliance on historic knowledge and statistical fashions might sometimes make it falter in predicting future market actions, significantly throughout excessive volatility or unexpected occasions. Furthermore, VaR might not encapsulate all danger sides, corresponding to liquidity or occasion dangers, which might sway portfolio efficiency. Moreover, VaR’s reliability hinges on the accuracy of knowledge and assumptions underlying its computation, necessitating buyers to complement it with methods corresponding to sensitivity evaluation and situation evaluation.
#statistical #instruments #danger #evaluation #investing
